Nsound Filters¶
Nsound currently provides two kinds of filters:
- Finite Impulse Response (FIR)
- Infinite Impulse Response (IIR)
Nsound provides both FIR and IIR filters for the types below:
- Low Pass
- High Pass
- Band Pass
- Band Reject (Or Notch filter)
FIR Filters¶
FIR filters are well behaved at all frequencies, they have symmetric phase distortion and are relatively computationally expensive.
Currently, Nsound designs FIR filters using a windowed sinc function and a Blackman window. See “DSP for Scientists and Engineer”, Chapter 16, equation 16-4.
Some of the basic documentation
- FilterLowPassFIR(sample_rate, n_order, fc)¶
- FilterHighPassFIR(sample_rate, n_order, fc)¶
- FilterBandPassFIR(sample_rate, n_order, fc_low, fc_high)¶
- FilterBandRejectFIR(sample_rate, n_order, fc_low, fc_high)¶
- sample_rate
- The number of samples per second.
- n_order
- The size of the filter kernel, the larger the order, the stronger the the rejection ouside of the pass band.
- fc
- The filter cut off frequency in Hz.
- fc_low
- The lower filter cut off frequency in Hz
- fc_high
- The high filter cut off frequency in Hz
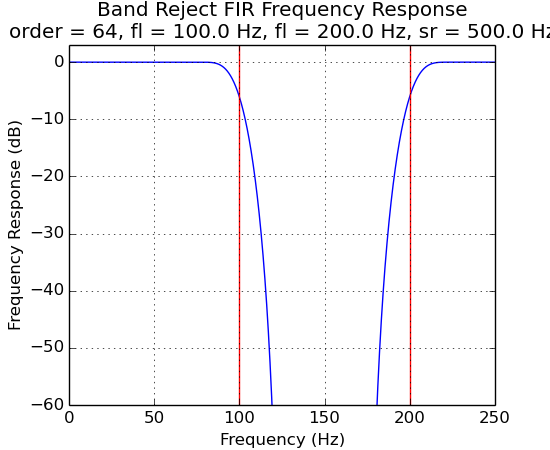
FIR Filter Frequency Response¶
Frequency responses for FIR filters:
import Nsound as ns
f1 = ns.FilterLowPassFIR(500.0, 64, 100.0)
f2 = ns.FilterHighPassFIR(500.0, 64, 100.0)
f3 = ns.FilterBandPassFIR(500.0, 64, 100.0, 200.0)
f4 = ns.FilterBandRejectFIR(500.0, 64, 100.0, 200.0)
f1.plot()
f2.plot()
f3.plot()
f4.plot()

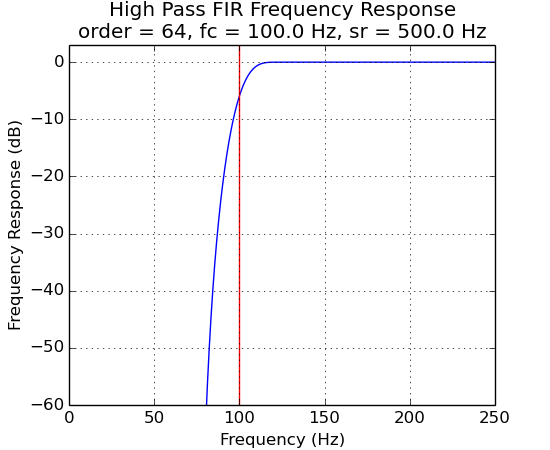

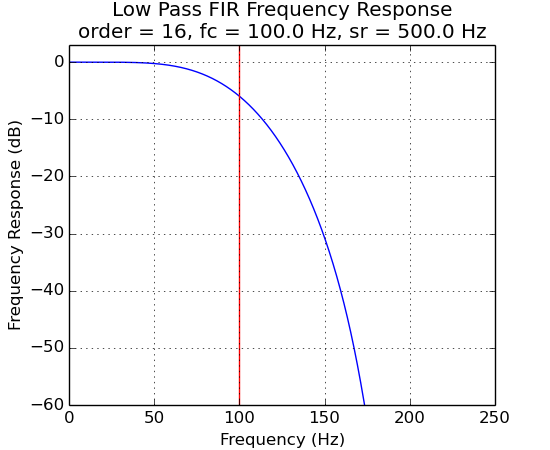
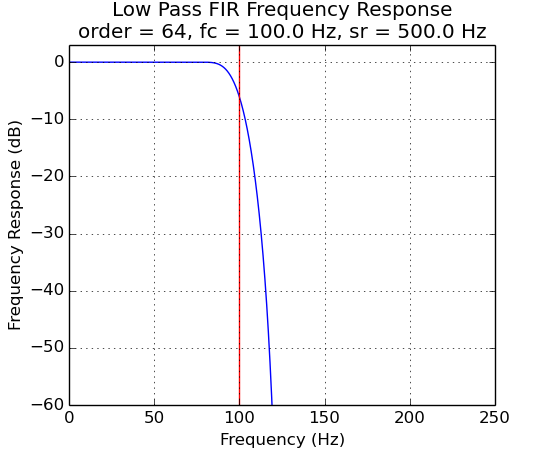
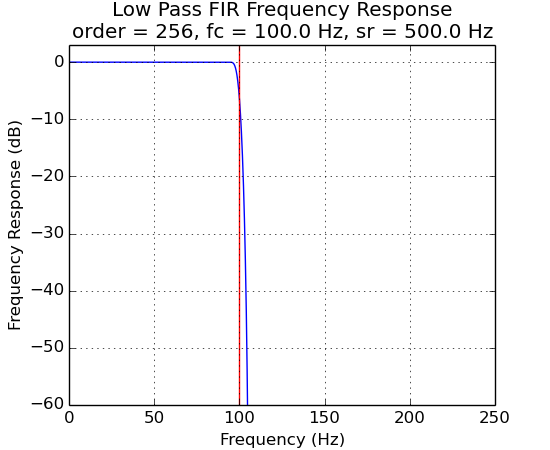
FIR Filter Frequency Response vs Filter Order¶
The plots below demonstrate the effects of filter order.
import Nsound as ns
f1 = ns.FilterLowPassFIR(500.0, 16, 100.0)
f2 = ns.FilterLowPassFIR(500.0, 64, 100.0)
f3 = ns.FilterLowPassFIR(500.0, 256, 100.0)
f4 = ns.FilterLowPassFIR(500.0, 1024, 100.0)
f1.plot()
f2.plot()
f3.plot()
f4.plot()

IIR Filters¶
IIR filters are not stable for all orders and cut off frequencies, they have asymmetrical phase distortion, but they are computationally inexpensive compared to FIR designs (because they perform far fewer multiplications).
Currently, Nsound designs IIR filters using Chebyshev type 1, ripples in the pass band. See “DSP for Scientists and Engineers”, Chapter 20, Table 20-4, 20-5. If the ripple percent parameter is set to 0.0, then the filter is maximally flat and equilavent to a Butterworth filter. Consider using 0.005 (0.5%) as the ripple percent, this acchives a sharper roll off with little ripple.
IIR Filter Frequency Response¶
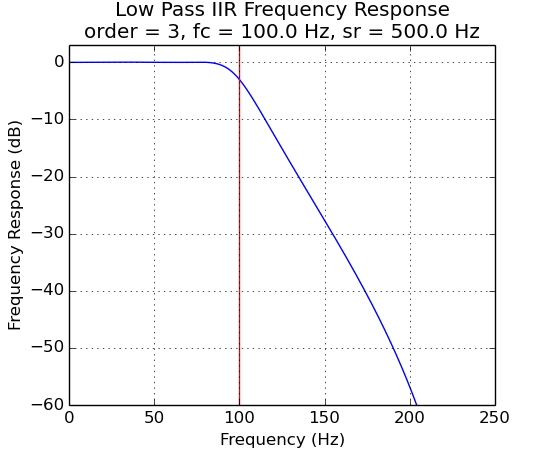
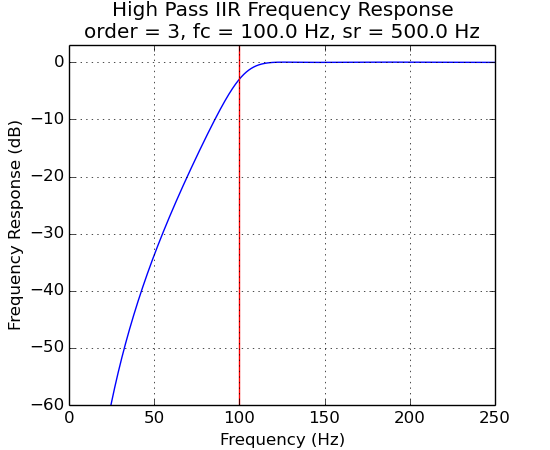
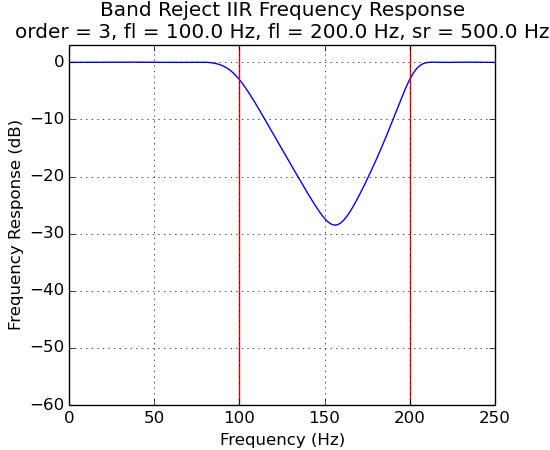
Frequency responses for IIR filters:
import Nsound as ns
ripple = 0.005
f1 = ns.FilterLowPassIIR(500.0, 4, 100.0, ripple)
f2 = ns.FilterHighPassIIR(500.0, 4, 100.0, ripple)
f3 = ns.FilterBandPassIIR(500.0, 4, 100.0, 200.0, ripple)
f4 = ns.FilterBandRejectIIR(500.0, 4, 100.0, 200.0, ripple)
f1.plot()
f2.plot()
f3.plot()
f4.plot()

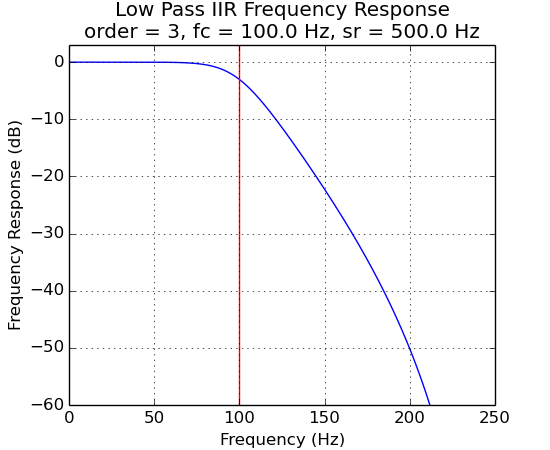
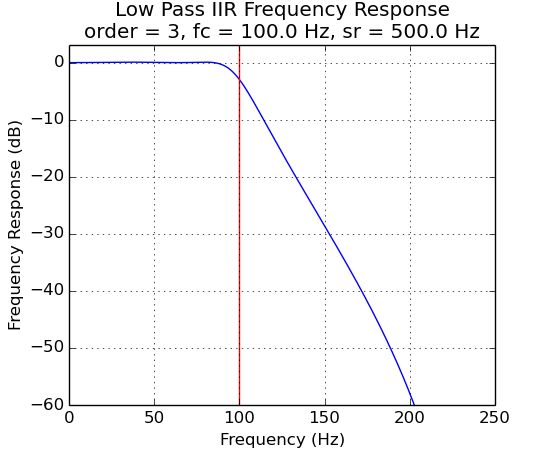
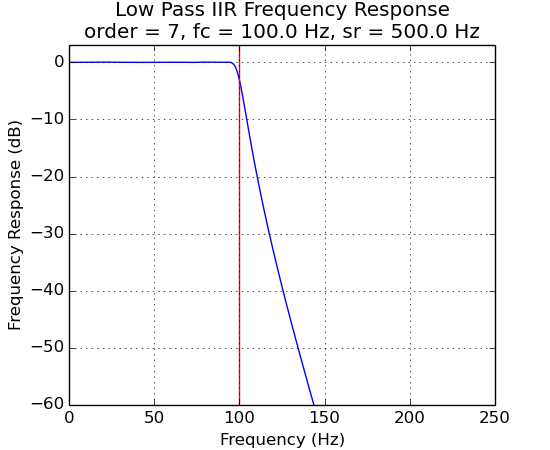
IIR Filter Frequency Response vs Filter Order¶
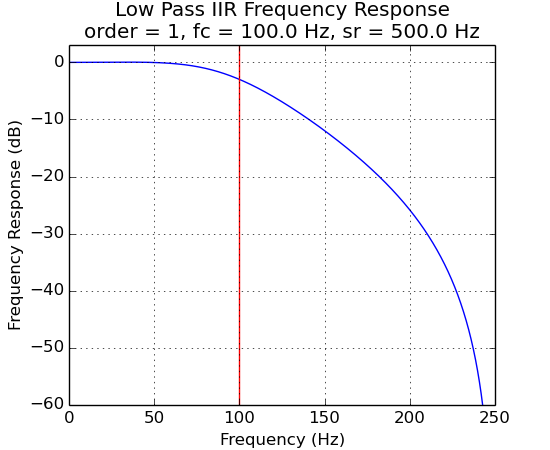
The plots below demonstrate the effects of filter order.
import Nsound as ns
ripple = 0.005
f1 = ns.FilterLowPassIIR(500.0, 2, 100.0, ripple)
f2 = ns.FilterLowPassIIR(500.0, 4, 100.0, ripple)
f3 = ns.FilterLowPassIIR(500.0, 8, 100.0, ripple)
f4 = ns.FilterLowPassIIR(500.0, 16, 100.0, ripple)
f1.plot()
f2.plot()
f3.plot()
f4.plot()


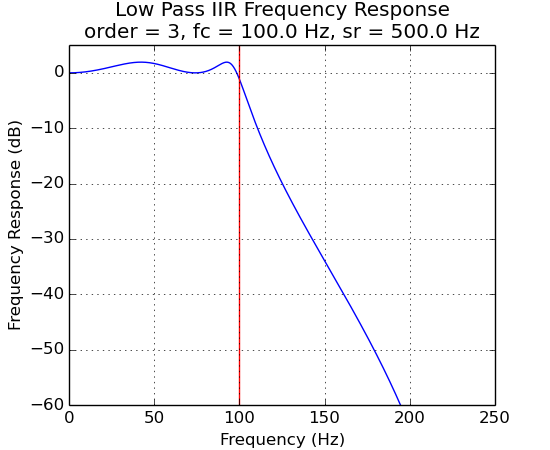
IIR Filter Frequency Response vs Ripple Percent¶
The plots below demonstrate the effects of filter order.
import Nsound as ns
f1 = ns.FilterLowPassIIR(500.0, 4, 100.0, 0.000)
f2 = ns.FilterLowPassIIR(500.0, 4, 100.0, 0.005)
f3 = ns.FilterLowPassIIR(500.0, 4, 100.0, 0.010)
f4 = ns.FilterLowPassIIR(500.0, 4, 100.0, 0.200)
f1.plot()
f2.plot()
f3.plot()
f4.plot()